Solution:
Let ABCD be a square with A(-1,2) and B(-1,2) (3,2). And Point O is the point where AC and BD intersect.
Now find the coordinates of the points B and D.
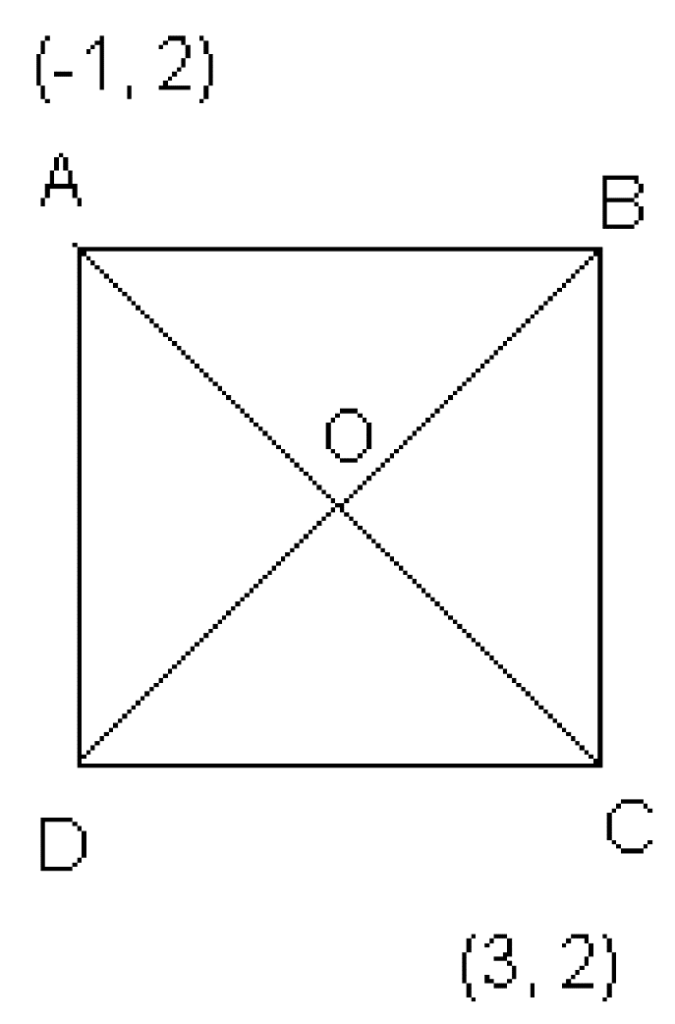
Step 1: Find coordinates of point O and distance between A and C.
As we know, the diagonals of a square are equal and bisect each other.
AC= √[(3 + 1)2 + (2 – 2)2] = 4
The coordinates of O can be found using the formula below:
x = (3 – 1)/2 = 1 and y = (2 + 2)/2 = 2
So, O(1,2)
Step 2: Using the Pythagoras theorem find the side of the square
Let a be the square’s side, and AC = 4.
From the right angle triangle, ACD,
a = 2√2
As a result, each square’s side= 2√2
Step 3: Find coordinates of point D
AD and CD length measure are equated.
Assume D’s coordinate are (x1, y1)
AD = √[(x1 + 1)2 + (y1 – 2)2]
When both sides are squared,
AD2 = (x1 + 1)2 + (y1 – 2)2
In the same way, CD2 = (x1 – 3)2 + (y1 – 2)2
Because all of the sides of a square are equal, therefore AD = CD
(x1 + 1)2 + (y1 – 2)2 = (x1 – 3)2 + (y1 – 2)2
x12 + 1 + 2x1 = x12 + 9 – 6x1
8x1 = 8
x1 = 1
By using the value of x, we can calculate the value of y1 as follows.
From step 2: each square’s side = 2√2
CD2 = (x1 – 3)2 + (y1 – 2)2
8 = (1 – 3)2 + (y1 – 2)2
8 = 4 + (y1 – 2)2
y1 – 2 = 2
y1 = 4
As a result, D = (1, 4)
Step 4: Find coordinates of point B
From the BOD line segment
B’s coordinates can be calculated using O’s coordinates, as follows:
We had already calculated as O = (1, 2)
Say B = (x2, y2)
For BD;
1 = (x2 + 1)/2
x2 = 1
And 2 = (y2 + 4)/2
=> y2 = 0
As a result, the coordinates of the required points are as B = (1,0) and D = (1,4)
