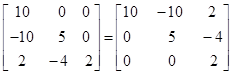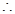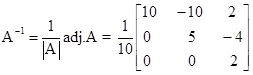$\left[\begin{array}{lll}1 & 2 & 3 \\ 0 & 2 & 4 \\ 0 & 0 & 5\end{array}\right]$

Solution:

Let $\mathrm{A}=\left[\begin{array}{lll}1 & 2 & 3 \\ 0 & 2 & 4 \\ 0 & 0 & 5\end{array}\right]$

$|A|=\left|\begin{array}{lll}1 & 2 & 3 \\ 0 & 2 & 4 \\ 0 & 0 & 5\end{array}\right|=1(10)-2(0)+3(0)=10 \neq 0$

Therefore,
$A^{-1}$ exists

A₁₁ = 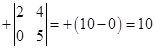,  A₁₂ = ,

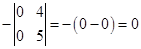A₁₃ = 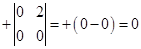,   A₂₁ = ,

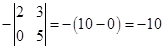A₂₂ = 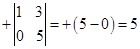,   A₂₃ = ,

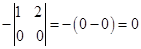A₃₁ = 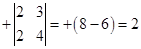,   A₃₂ = ,

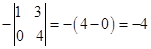A₃₃ =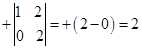 

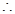 adj. A =