![]()
Solution:-
From the given data,
draw the table of the given data and append other columns after calculations.

Now calculate Mean for x,
Mean ![]()
Where, n = number of terms ![]()
![]()
Variance for x= ![Rendered by QuickLaTeX.com \frac{1}{{{n}^{2}}}\left[ N\sum x_{1}^{2}-{{\left( \sum {{x}_{i}} \right)}^{2}} \right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-c802603d2dd59d8f961f5b119c552f2b_l3.png)
![]()
![]()
![]()
WKT Standard deviation = ![]()
![]()
![]()
So, co-efficient of variation ![]()
![]()
![]()
Calculate Mean for y,
Mean ![]()
Where, n = number of terms
![]()
![]()
Variance for y
![Rendered by QuickLaTeX.com =\frac{1}{{{n}^{2}}}\left[ N\sum y_{1}^{2}-{{\left( \sum {{y}_{i}} \right)}^{2}} \right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-5d7445ea04dcbd5a7babcd5b051d0685_l3.png)
![]()
![]()
![]()
![]()
WKT Standard deviation ![]()
![]()
![]()
So, co-efficient of variation ![]()
![]()
![]()
Compare C.V. of X and Y.
C.V of X > C.V. of Y
So, Y is more stable than X.

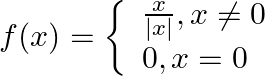 . Show that
. Show that 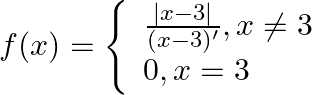 . Show that
. Show that