Answer: $\begin{array}{l} \frac{2}{{\sqrt 7 }} = \frac{2}{{\sqrt 7 }} \times \frac{{\sqrt 7 }}{{\sqrt 7 }}\\ = > \frac{2}{7}\sqrt 7 \end{array}$ is a rational number. p and q are some integers...
Show that
Prove that 5√2 is irrational.
Answer: Consider, 5√2 - rational number. ∴ 5√2 = p/q, where p and q are some integers and HCF(p, q) = 1 5√2q = p (5√2q)2 = p2 2(25q2) = p2 p2 is divisible by 2 p is divisible by 2 p = 2m, where m is...
Show that (5 – 2√3) is irrational.
Answer: Consider, x = 5 - 2√3 be a rational number. x = 5 - 2√3 x2 = (5 - 2√3)2 x2 = 52 + (2√3) 2 – 2(5) (2√3) x2 = 25 + 12 – 20√3 x2 – 37 = – 20√3 => $\frac{37-{{x}^{2}}}{20}$ => √3 x...
Prove that (4 – 5√2) is irrational.
Answer: Consider, x = 4 - 5√2 be a rational number. x = 4 - 5√2 x2 = (4 - 5√2)2 x2 = 42 + (5√2)2 – 2(4) (5√2) x2 = 16 + 50 – 40√2 x2 – 66 x2 = – 40√2 => $\frac{66-{{x}^{2}}}{40}$ => √2 x is a...
Prove that (2 √3 – 1) is irrational.
Answer: Consider, x = 2 √3 – 1 be a rational number. x = 2 √3 – 1 x2 = (2 √3 – 1)2 x2 = (2 √3 )2 + (1)2 – 2(2 √3)(1) x2 = 12 + 1 - 4 √3 x2 – 13 = - 4 √3 $\frac{13-{{x}^{2}}}{4}=>\sqrt{3}$ x -...
State whether the given statement is true or false: (i) The sum of a rational and an irrational is irrational (ii) The product of a rational and an irrational is irrational
Answers: (i) The sum of a rational and an irrational is irrational The given statement is True. (ii) The product of a rational and an irrational is irrational The given statement is True....
State whether the given statement is true or false: (i) The sum of two irrationals is an irrational (ii) The product of two irrationals is an irrational
Answers: (i) The sum of two irrationals is an irrational The given statement is False. Reason: 2 + √3 and 2 - √3 are two irrational numbers. But their sum is 4, which is a rational number. (ii) The...
State whether the given statement is true or false: (i) The sum of two rationals is always rational (ii) The product of two rationals is always rational
Answers: (i) The sum of two rationals is always rational The given statement is True. (ii) The product of two rationals is always rational The given statement is True.
(i) Give an example of two irrationals whose sum is rational. (ii) Give an example of two irrationals whose product is rational.
Answers: (i) Consider, (2 + √3), (2 - √3) be two irrationals. ∴ (2 + √3) + (2 - √3) = 4 = rational number (ii) Consider, 2 √3, 3 √3 be two irrationals. ∴ 2 √3 × 3 √3 = 18 = rational...
Prove that 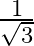 is irrational.
is irrational.
Answer: Consider, $\frac{1}{\sqrt{3}}$ be rational. $\frac{1}{\sqrt{3}}=\frac{a}{b}$ , where a, b are positive integers having no common factor other than 1 ∴√3 = $\frac{b}{a}$ Since a, b are...
Prove that each of the following number is irrational: √3 + √5
Answer: Consider, √3 + √5 be rational. ∴√3 + √5 = a, where a is rational. ∴ √3 = a - √5 Square on both sides, 3 = (a - √5) 2 = a 2 + 5 - 2√5a $\sqrt{5}=\frac{{{a}^{2}}+2}{2a}$ This is impossible...
Prove that each of the following numbers is irrational: (i) 3/√5 (ii) 2 – 3√5
Answers: (i) Consider, 3/√5 be rational. 1/3 × 3/√5 = 1/√5 is rational This contradicts the fact that 1/√5 is irrational. ∴1 × √5/√5 × √5 = 1/5 √5 If 1/√5 is irrational, then 1/5√5 is rational...
Prove that each of the following numbers is irrational: (i) 5 + 3√2 (ii) 3√7
Answers: (i) Consider, 5 + 3√2 be rational. 5 and 5 + 3√2 are rational. ∴ (5 + 3√2 – 5) = 3√2 = rational ∴ 1/3 × 3√2 = √2 = rational This contradicts the fact that √2 is irrational. The...
Prove that each of the following numbers is irrational: (i) 3 + √2 (ii) 2 + √5
Answers: (i) Consider, 3 + √2 be rational. 3 and 3 + √2 are rational. ∴ 3 + √2 – 3 = √2 = rational This contradicts the fact that √2 is irrational. The contradiction arises by assuming 3 + √2 is...
Prove that each of the following numbers is irrational: (i) √6 (ii) 2 – √3
Answers: (i) Consider, √6 = √2 × √3 be rational. √2, √3 are both rational. This contradicts the fact that √2, √3 is irrational. The contradiction arises by assuming √6 is rational. √6 is irrational....
Classify the following numbers as rational or irrational: (i) √21 (ii) 
Answers: (i) √21 = √3 × √7 is an irrational number because √3 and √7 are irrational and prime numbers. (ii) ${}^{3}\sqrt{3}$ is an irrational number because 3 is a prime number. So, √3 is an...
Classify the following numbers as rational or irrational: (i) 1.535335333 (ii) 3.121221222
Answers: (i) 1.535335333… is an irrational number because it is a non-terminating and non-repeating decimal. (ii) 3.121221222… is an irrational number because it is a non-terminating and...
Classify the following numbers as rational or irrational: (i) 5.636363 (ii) 2.040040004
Answers: (i) 5.636363… is a rational number because it is a non-terminating and non-repeating decimal. (ii) 2.040040004… is an irrational number because it is a non-terminating and non-repeating...
Classify the following numbers as rational or irrational: 
Answers: (i) π is an irrational number because it is a non-repeating and non-terminating decimal. (ii) $3.\overline{142857}$ is a rational number because it is a repeating decimal.
Classify the following numbers as rational or irrational: 
Answers: (i) $\frac{22}{7}$ is a rational number because it is of the form of $\frac{p}{q}$ where q ≠ 0. (ii) 3.1416 is a rational number because it is a terminating decimal.
Define real numbers
Real numbers: The numbers which are positive or negative, whole numbers or decimal numbers and rational numbers or irrational number are called real numbers. Example: 2, 1/3 ,√2 , -3 etc.
Define (i) rational numbers (ii) irrational numbers
(i) Rational numbers: The numbers of the form ????/???? where ????, ???? are integers and ???? ≠ 0 are called rational numbers. Example: 2/3 (ii) Irrational numbers: The numbers which when expressed...
Find the maximum number of students among whom 1001 pens and 910 pencils can be distributed in such a way that each student gets the same number of pens and the same number of pencils.
Answer: Total number of pens = 1001 Total number pencils = 910 ∴ Maximum number of students who get the same number of pens and pencils = HCF (1001, 910) Using prime factorization, 1001 = 11 × 91...
