Solution
Assume ![]() denotes boy and
denotes boy and ![]() denote girl.
denote girl.
Then, the sample space of the given experiment is ![]() Let
Let ![]() be the event that ‘both are girls’.
be the event that ‘both are girls’.
![]()
![]()
(i) Let ![]() be the event that ‘the youngest is a girl’.
be the event that ‘the youngest is a girl’.
![]()
![]()
Now, ![]()
![]()
Now, we know that by relation of conditional probability,
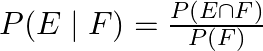
 and (ii)]
and (ii)]![]()
(ii) Assume ![]() be the event that ‘at least one is a girl’.
be the event that ‘at least one is a girl’.
![]()
![]()
Now, ![]()
![]()
Now, we know that by relation of conditional probability,
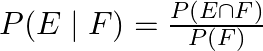
![Rendered by QuickLaTeX.com \[\begin{aligned}&\Rightarrow \mathrm{P}(\mathrm{E} \mid \mathrm{H})=\frac{\mathrm{P}(\mathrm{E} n \mathrm{H})}{\mathrm{P}(\mathrm{H})}=\frac{1 / 4}{3 / 4}=\frac{1}{3} &\Rightarrow \mathrm{P}(\mathrm{E} \mid \mathrm{H})=\frac{1}{3}\end{aligned}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-538a8812466ee39b4ccabadd722d9159_l3.png)
