Login/Sign Up
Home » A parallel plate capacitor made of circular plates each of radius has a capacitance . The capacitor is connected to a ac supply with an (angular) frequency of .(a) What is the rms value of the conduction current?(b) Is the conduction current equal to the displacement current?
A parallel plate capacitor made of circular plates each of radius \mathbf{R}=\mathbf{6 . 0} \mathbf{~ c m} has a capacitance C=100 \mathrm{pF}. The capacitor is connected to a 230 \mathrm{~V} ac supply with an (angular) frequency of 300 \mathrm{rad} \mathrm{s}^{-1}.
(a) What is the rms value of the conduction current?
(b) Is the conduction current equal to the displacement current?
CBSE | Class 12 | Electromagnetic Waves | NCERT | Physics
A parallel plate capacitor made of circular plates each of radius \mathbf{R}=\mathbf{6 . 0} \mathbf{~ c m} has a capacitance C=100 \mathrm{pF}. The capacitor is connected to a 230 \mathrm{~V} ac supply with an (angular) frequency of 300 \mathrm{rad} \mathrm{s}^{-1}.
(a) What is the rms value of the conduction current?
(b) Is the conduction current equal to the displacement current?

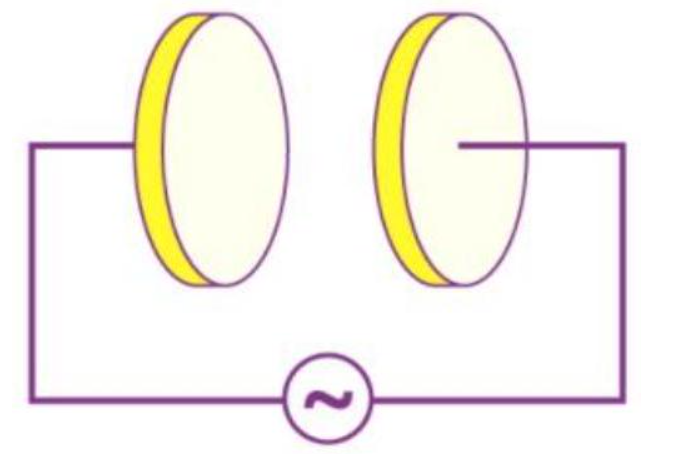
Solution:

Radius of each circular plate is given as 0.06m

Capacitance of a parallel plate capacitor is given as \mathrm{C}=100 \mathrm{pF}=100 \times 10^{-12} \mathrm{~F}

Supply voltage is given as V=230 \mathrm{~V}

Angular frequency is given as \omega=300 \mathrm{rad} \mathrm{s}^{-1}

(a) Rms value of conduction current is represented by the equation,

I=\frac{V}{X_{c}}

Where,

X_{c}= Capacitive reactance =\frac{1}{\omega C}

\therefore I=V \times \omega C

=230 \times 300 \times 100 \times 10^{-12}

=6.9 \times 10^{-6} \mathrm{~A}

=6.9 \mu \mathrm{A}

As a result, 6.9 \mu \mathrm{A} is the rms value of conduction current.

(b) Yes, conduction current is equivalent to displacement current.

i

More Material